Lecture 16: ADTs, Sets, Maps, Binary Search Trees

10/2/2020

Abstract Data Types

Abstract Data Types (ADT)

• An Abstract Data Type (ADT) is defined only by its operations, not by its implementation
• Deque ADT:
  • addFirst
  • addLast
  • isEmpty
  • size
  • printDeque
  • removeFirst
  • removeLast
  • get

Another example of an ADT: The Stack

• The Stack ADT supports the following operations
  • push(int x): Puts x on top of the stack
  • int pop(): Removes and returns the top item from the stack
• Which implementation do you think would result in faster overall performance?
  • Linked List
  • Array
• Both are about hte same. No resizing for linked lists, so probably a little faster

GrabBag ADT

• The GrabBag ADT supports the following operations:
  • insert(int x): Inserts x into the grab bag
  • int remove(): Removes a random item from the bag
  • int sample(): Samples a random item from the bag
  • int size(): Number of items in the bag
• In this case, Array will result in faster performance than Linked List

Abstract Data Types in Java

• Syntax differentiation between abstract data types and implementations
  • Interfaces in Java aren't purely abstract and can contain some implementation details, e.g. default methods
• Example: List<Integer> L = new ArrayList<>();

Collections

• Among the most important features in java.util library are those that extend the Collection interface
  • Lists of things
  • Sets of things
  • Mappings between items
    • Maps also known as associate arrays, associative lists, symbol tables, dictionaries

Java Libraries

• The built-in java.util package provides a number of useful:
  • Interfaces: ADTs (lists, sets, maps, priority queues, etc)
  • Implementations: Concrete classes you can use

Binary Search Trees

AnLysis of an OrderedLinkedListSet

• We implemented a set based on unordered arrays. For the order linked list set implementation, name an operation that takes worst case linear time, i.e. Theta(N)
  • Both contains and add will take linear time

Optimization: Extra Links

• Fundamental Problem: Slow search, even though it's in order
  • Add (random) express lanes. Skip List (won't discuss in 61B)

Optimization: Change the Entry Point

• Fundamental Problem: Slow search, even though it's in order
  • Move pointer to middle and flip left links. Halved search time!
  
  • How do we do even better?
  

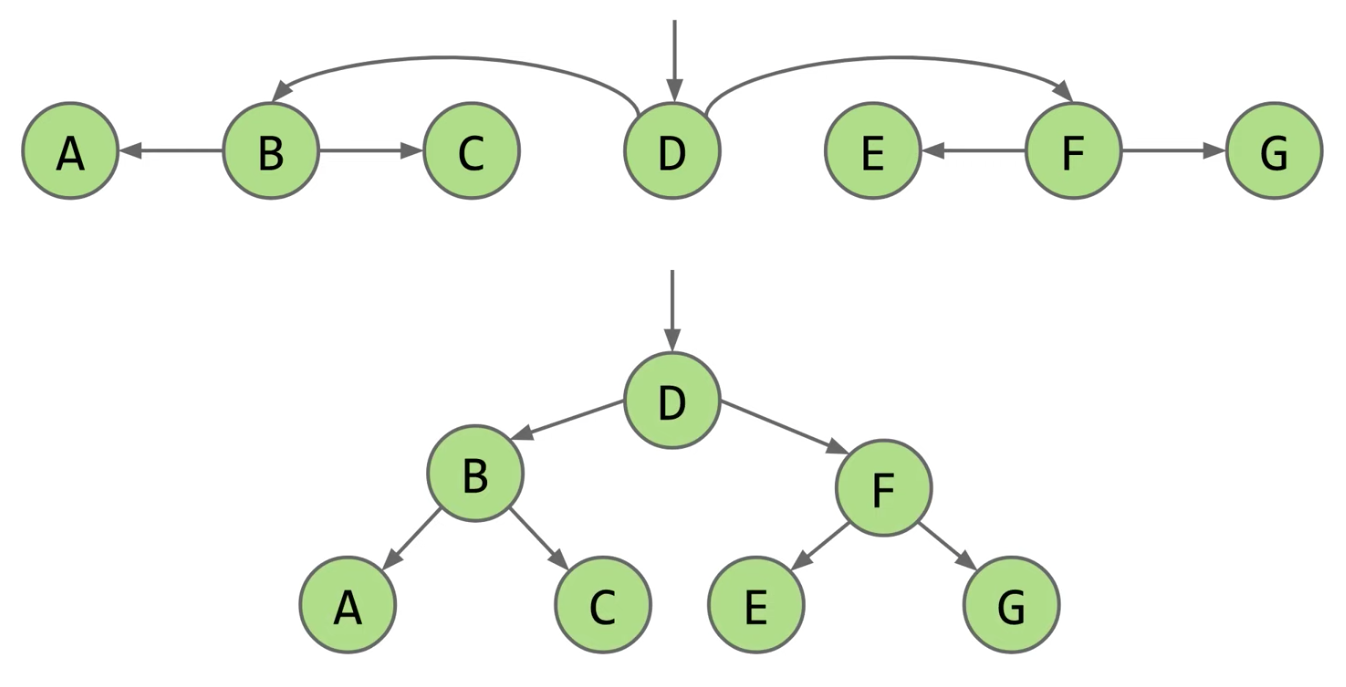
BST Definitions

Tree

• A tree consists of
  • A set of nodes
  • A set of edges that connect those nodes
    • Constraint: There is exactly one path between any two nodes

Rooted Trees and Rooted Binary Trees

• In a rooted tree, we call one node the root
  • Every node N except the root has exactly one parent, defined as the first node on the path from N to the root
  • A node with no child is called a leaf
• In a rooted binary tree, every node has either 0, 1, or 2 children (subtrees)

Binary Search Trees

• A binary search tree is a rooted binary tree with the BST property
• BST Property. For every node X in the tree
  • Every key in the left subtree is less than X's key
  • Every key in the right subtree is greater than X's tree
• Ordering must be complete, transitive, and antisymmetric. Given keys p and q:
  • Exactly one of p < q and q < p are true
  • p < q and q < r implies p < r
• One consequence of these rules: No duplicate keys allowed!
  • Keep things simple. Most real world implementations follow this rule

BST Operations: Search

Finding a searchKey in a BST

• If searchKey returns T.key, return
  • If searchKey < T.key, search T.left
  • If searchKey > T.key, search T.right

static BST find(BST T, key sk) {
    if (T == null)
        return null;
    if (sk.equals(T.key))
        return T;
    else if (sk < T.key)
        return find(T.left, sk);
    else
        return find(T.right, sk);
}

• What is the runtime to complete a search on a "bushy" BST in the worst case, where N is the number of nodes?
  • Answer is Theta(log N)
  • Height of the tree is ~log_2(N)

BSTs

• Bushy BSTs are extremely fast
• Much computation is dedicated towards finding things in response to queries
  • It's a good thing that we can do such queries almost for free

BST Operations: Insert

Inserting a new key into a BST

• Search for key
  • If found, do nothing
  • If not found
    • Create a new node
    • Set appropriate link

static BST insert(BST T, Key ik) {
    if (T == null)
        return new BST(ik);
    if (ik < T.key)
        T.left = insert(T.left, ik);
    else if (ik > T.key)
        T.right = insert(T.right, ik);
    return T;
}

BST Operation: Delete

Deleting from a BST

• 3 Cases:
  • Deletion key has no children
  • Deletion key has one child
  • Deletion key has two children

Case 1: Deleting from a BST: Key with no Children

• Deletion key has no children
  • Just sever hte parent's link
  • Garbage collected

Case 2: Deleting from a BST: Key with one Child

• Goal: Maintain BST property
  • Key's child definitely larger than parent
    • Safe to just move that child into key's spot
• Thus: Move key's parent's pointer to key's child
  • Key will be garbage collected (along with its instance variables)

Case 3: Deleting from a BST: Deletion with two Children

• Goal:
  • Find a new root node
  • Must be > than everything in left subtree
  • Must be < than everything in right subtree
• Choose either predecessor or successor
  • Delete predecessor (the largest key smaller than the removed key) or successor (the smallest key larger than the removed key), and stick new copy in the root position
    • This deletion guaranteed to be either case 1 or 2
  • This strategy is sometimes known as "Hibbard deletion"

Sets vs. Maps, Summary

Sets vs. Maps

• Can think of the BST as representing a Set
• But what if we wanted to represent a mapping of word counts?
• To represent maps, just have each BST node store key/value pairs
• Note: No efficient way to look up by value
  • Example: Cannot find all the keys with value = 1 without iterating over ALL nodes. This is fine.

Summary

• Abstract data types are defined in terms of operations, not implementation
• Several useful ADTs: Disjoint Sets, Map, Set, List
  • Java provides Map, Set, List interfaces, along with several implementations
• We've seen two ways to implement a Set (or Map): ArraySet and using a BST
  • ArraySet: Theta(N) operations in the worst case
  • BST: Theta(log N) operations if tree is balanced
• BST implementations:
  • Search and insert are straightforward (but insert is a little tricky)
  • Deletion is more challenging. Typical approach is "Hibbard deletion"

BST Implementation Tips

Tips for BST Lab

• Code from class was "naked recursion". Your BSTMap will not be
• For each public method, e.g. put(K key, V value), create a private recursive method, e.g. put(K key, V value, Node n)
• When inserting, always set left/right pointers, even if nothing is actually changing
• Avoid "arms length base cases". Don't check if left or right is null!

CSM Review

• A list is an ordered sequence of items: like an array, but without worrying about the length or size

interface List<E> {
  boolean add(E element);
  void add(int index, E element);
  E get(int index);
  int size();
}

• Maps (Dictionary)
  • Notes:
    • Keys are unique
    • Values don't have to be unique
    • Key lookup: O(1)
  • A map is a collection of key-value mappings, like a dictionary in Python
  • Like a set, the keys in a map are unique

interface Map<K, V> {
  V put(K key, V value);
  V get(K key);
  boolean containsKey(Object key);
  Set<K> keySet();
}

• Sets
  • Notes:
    • Unordered collection of unique items
    • Set operations are O(1)
  • A set is an unordered collection of unique elements

interface Set<E> {
  boolean add(E element);
  boolean contains(Object object);
  int size();
  boolean remove(Object object);
}

• Stacks and Queues
  • Stack
    • "First in Last out"
  • Queue
    • "First in First out"