Lecture 17: B-Trees (2-3, 2-3-4 Trees)
10/5/2020
BST Tree Height
BST Tree Height
- Trees range from best-case "bushy" to worst-case "spindly"
- Height varies dramatically among the two
- Theta(log N) for bushy vs Theta(N) for spindly
- Performance of operations on spindly trees can be just as bad as a linked list!
- A worst case (spindly tree) has a height that grows exactly linearly - Theta(N)
- A best case (bushy tree) has a tree height that grows exactly logarithmically - Theta(log N)
The Usefulness of Big O
- Big O is a useful idea:
- Allows us to make simple blanket statements, e.g. can just say "binary search is O(log N)" instead of "binary search is Theta(log N) in the worst case"
- Sometimes don't know the exact runtime, so use O to give an upper bound
- Example: Runtime for finding shortest route that goes to all world cities is O(2^N). There might be a faster way, but nobody knows one yet
- Easier to write proofs for Big O than Big Theta, e.g. finding runtime of mergesort, you can round up the number of items to the next power of 2. A little beyond the scope of the course.
Height and Depth
- Height and average depth are important properties of BSTs
- The "depth" of a node is how far it is from the root
- The "height" of a tree is the depth of its deepest leaf
- The "average depth" of a tree is the average depth of a tree's nodes
Height, Depth, and Runtime
- Height and average depth determine runtimes for BST operations
- The "height" of a tree determines the worst case runtime to find a node
- The "average depth" determines the average case runtime to find a node
Important Question: What about real world BSTs?
- BSTs have:
- Worst case Theta(N) height
- Best case Theta(log N) height
- One way to approximate real world BSTs is to consider randomized BSTs
- Nice Property. Random trees have Theta(log N) average depth and height
- In other words: Random trees are bushy, not spindly
Randomized Trees: Mathematical Analysis
- Average Depth. If N distinct keys are inserted into a BST, the expected average depth is ~ 2 ln N
- Thus, average runtime for contains operation is Theta(log N) on a tree built with random inserts
- Tree Height. If N distinct keys are inserted in random order, expected tree height is ~ 4.311 ln N
- Thus, worst case runtime for contains operation is Theta(log N) on a tree built with random inserts
- BSTs have:
- Worst case Theta(N) height
- Best case Theta(log N) height
- Theta(log N) height if constructed via random inserts
- In real world applications we expect both insertion and deletion
- Can show that random trees including deletion are still Theta(log N) height
Good News and Bad News
- Good news: BSTs have great performance if we insert items randomly
- Performance is Theta(log N) per operation
- Bad news: We can't always insert our items in a random order
- Data comes in over time, don't have all at once
B-trees / 2-3 trees / 2-3-4 trees
Avoiding Imbalance through Overstuffing
- The problem is adding new leaves at the bottom
- Crazy idea: never add new leaves at the bottom
- Tree can never get imbalanced
- Avoid new leaves by "overstuffing" the leaf nodes
- "Overstuffed tree" always has balanced height, because leaf depths never change
- Overstuffed trees are a logically consistent but very weird data structure
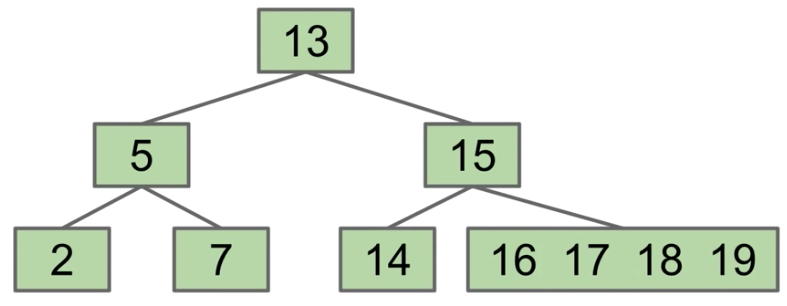
- contains(18):
- 18 > 13? Yes, go right
- 18 > 15? Yes, go right
- 16 = 18? No
- 17 = 18? No
- 18 = 18? Yes! Found it
- Problem with this idea? Degenerates into linked list
Revising Our Overstuffed Tree Approach: Moving Items Up
- Height is balanced, but we have a new problem
- Leaf nodes can get too juicy
- Solution?
- Set a limit L on the number of items, say L=3
- If any node has more than L items, give an item to parent
- Which one? Let's say (arbitrarily) the left-middle
- What's the problem now?
- 16 is to the right of 17
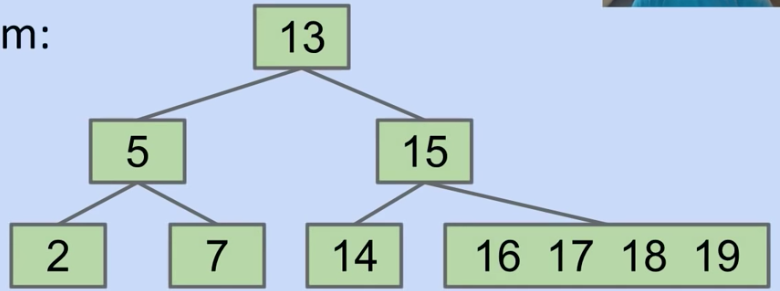
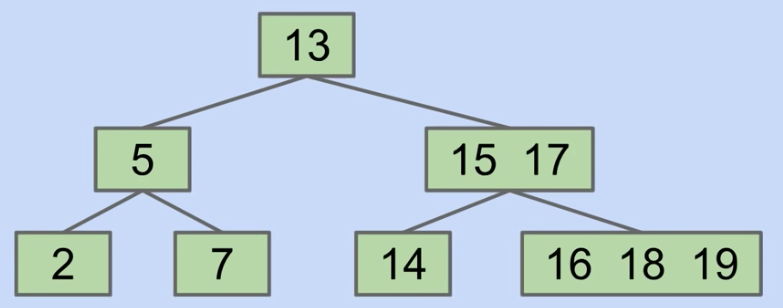
Revising Overstuffed Tree Approach: Node Splitting
- Solution?
- Set a limit L on the number of items, say L=3
- If any node has more than L items, give an item to parent
- Pulling item out of full node splits it into left and right
- Parent node now has three children!

- This is a logically consistent and not so weird data structure
- Contains(18):
- 18 > 13, so go right
- 18 > 15, so compare vs. 17
- 18 > 17, so go right
- Examining a node costs us O(L) compares, but that's OK since L is constant
- What if a non=leaf node gets too full? Can we split that?
add: Chain Reaction

What Happens if the root is too full?

Perfect Balance
- Observation: Splitting-trees have perfect balance
- If we split the root, every node gets pushed down by exactly one level
- If we split a leaf or internal node, the height doesn't change
- All operations have guaranteed O(log N) time
THe Real Name for Splitting Trees is "B Trees"
- B-trees of order L=3 (like we used today) are also called a 2-3-4 tree or a 2-4 tree
- "2-3-4" refers to the number of children that a node can have
- B-trees of order L=2 are also called a 2-3 tree
- B-Trees are most popular in two specific contexts:
- Small L(L=2 or L=3)
- Used as a conceptually simple balanced search tree
- L is very large (say thousands)
- Used in practice for databases and file systems
B-tree Bushiness Invariants
Exercise
- No matter the insertion order you choose, resulting B-Tree is always bushy!
- May vary in height a little bit, but overall guaranteed to be bushy
B-Tree Invariants
- Because of the way B-Trees are constructed, we get two nice invariants
- All leaves must be the same distance from the source
- A non-leaf node with k items must have exactly k+1 children
- These invariants guarantee that our tree will be bushy
B-Tree Runtime Analysis
Height of a B-Tree with Limit L
- L: Max number of items per node
- Height: Between ~log_{L+1}(N) and ~log_2(N)
- Largest possible height is all non-leaf nodes have 1 item
- Smallest possible height is all nodes have L items
- Overall height is therefore Theta(log N)
Runtime for contains
- Runtime or contains:
- Worst case number of nodes to inspect: H + 1
- Worst case number of items to inspect per node: L
- Overall runtime: O(HL)
- Since H = Theta(log N), overall runtime is O(L log N)
- Since L is a constant, runtime is therefore O(log N)
- Bottom line: contains and add are both O(log N)
Summary
Summary
- BSTs have best case height Theta(log N) and worst case height Theta(N)
- Big O is not the same thing as worst case
- B-Trees are a modification of the binary search tree that avoids Theta(N) worst case
- Nodes may contain between 1 and L items
contains works almost exactly like a normal BSTadd works by adding items to existing leaf nodes
- If nodes are too full, they split
- Resulting tree has perfect balance. Runtime for operations is O(log N)
- Have not discussed deletion
- Have not discussed how splitting works if L > 3
- B-trees are more complex, but they can efficiently handle ANY insertion order





