Lecture 18: Red Black Trees

10/7/2020

The Bad News

• 2-3 trees (and 2-3-4 trees) are a real pain to implement, and suffer from performance problems. Issues include:
  • Maintaining different node types
  • Interconversion of nodes between 2-nodes and 3-nodes
  • Walking up the tree to split nodes

BST Structure and Tree Rotation

BSTs

• Suppose we have a BST with the numbers 1, 2, 3. Five possible BSTs
  • The specific BST you get is based on the insertion order
  • More generally, for N items, there are Catalan(N) different BSTs
• Given any BST, it is possible to move to a different configuration using "rotation"
  • In general, can move from any configuration to any other in 2n - 6 rotations

Tree Rotation Definition

• rotateLeft(G): Let x be the right child of G. Make G the new left child of x
  • Preserves search tree property. No change to semantics of tree
  • Can think of as temporarily G and P, then sending G down and left

• rotateRight(P): Let x be the left child of P. Make P the new right child of x
  • Can think of as temporarily merging G and P, then sending P down and right

Rotation for Balance

• Rotation:
  • Can shorten (or lengthen) a tree
  • Preserves search tree property

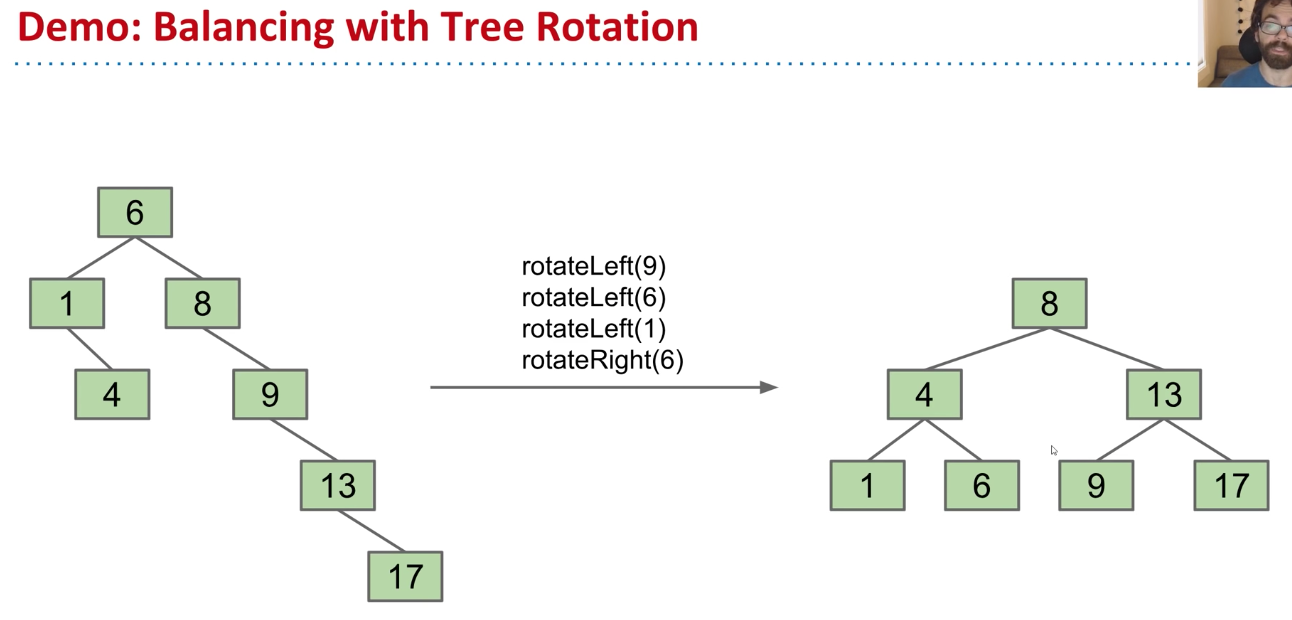
Rotation: An Alternate Approach to Balance

• Rotation:
  • Can shorten (or lengthen) a tree
  • Preserves search tree property
• Paying O(n) to occasionally balance a tree is not ideal. In this lecture, we''l see a better way to achieve balance through rotation

Red-Black Trees

Search Trees

• There are many types of search trees:
  • Binary search trees: Can balance using rotation, but we have no algorithms for doing so (yet)
  • 2-3 trees: Balanced by construction, i.e. no rotations required
• Let's try something clever, but strange
• Our goal: Build a BST that is structurally identical to a 2-3 tree
  • Since 2-3 trees are balanced, so will our special BSTs.

Representing a 2-3 Tree as a BST

• A 2-3 tree with only 2-nodes is trivial
  • BST is exactly the same!
• What do we do about 3-nodes?
  • Possibility 1: Create dummy "glue" nodes
    • Result is inelegant. Wasted link. Code will be ugly
  • Possibility 2: Create "glue" links with the smaller item off to the left
    • Idea is commonly used in practice

Left-Leaning Red Black Binary Search Tree (LLRB)

• A BST with left glue links that represent a 2-3 tree is often called a "Left Leaning Red Black Binary Search Tree" or LLRB
  • LLRBs are normal BSTs
  • There is a 1-1 correspondence between an LLRB and an equivalent 2-3 tree
  • The red is just a convenient fiction. Red links don't "do" anything special
  

Red Black Tree Properties

Left-Leaning Red Black Binary Search Tree (LLRB)

• Searching an LLRB tree for a key is easy
  • Treat it exactly like any BST

Left-Leaning Red Black Binary Search Tree (LLRB) Properties

• Some handy LLRB properties:
  • No node has two red links [otherwise it'd be analogous to a 4 node, which are disallowed in 2-3 trees]
  • Every path from root to a leaf has same number of black links [because 2-3 trees have the same number of links to every leaf]. LLRBs are therefore balanced
  • Logarithmic height

LLRB Construction

• Where do LLRBs come from?
  • Would not make sense to build a 2-3 tree, then convert it
  • Instead, it turns out we implement an LLRB insert as follows:
    • Insert as usual into a BST
    • Use zero or more rotations to maintain the 1-1 mapping

Maintaining 1-1 Correspondence Through Rotations

The 1-1 Mapping

• There exists a 1-1 mapping between:
  • 2-3 Tree
  • LLRB
• Implementation of an LLRB is based on maintaining this 1-1 correspondence
  • When performing LLRB operations, pretend like you're a 2-3 tree
  • Preservation of the correspondence will involve tree rotations

Design Task 1: Insertion Color

• Always use a red link when adding onto a leaf

Design Task 2: Insertion on the Right

• Right links aren't allowed, so rotateLeft
• Likewise, left links aren't allowed, so rotateRight

New Rule: Representation of Temporary 4-Nodes

• We will represent temporary 4-nodes as BST nodes with two red links
  • This state is only temporary, so temporary violation of "left leaning" is ok

Design Task 3: Double insertion on the left

• When double inserting on the left, rotate the node to the right

Design Task 4: Splitting Temporary 4-nodes

• Suppose we have the LLRB includes a temporary 4 node
  • To fix this, flip the colors of all edges touching the node
    • Note: This doesn't change the BST structure/shape

That's it!

• We've just invented the red-black BST
  • When inserting: Use a red link
  • If there is a right leaning "3-node", we have a Left Leaning Violation
    • Rotate left the appropriate node to fix
  • If there are two consecutive left links, we have an Incorrect 4 Node VIolation
    • Rotate right the appropriate node to fix
  • If there are any nodes with two red children, we have a Temporary 4 Node
    • Color flip the node to emulate the split operation
• Cascading operations
  • It is possible that a rotation or flip operation will cause an additional violation that needs fixing

LLRB Runtime and Implementation

LLRB Runtime

• The runtime analysis for LLRBs is simple if you trust the 2-3 tree runtime
  • LLRB tree has height O(log N)
  • Contains is trivially O(log N)
  • Insert is O(log N)
    • O(log N) to add the new node
    • O(log N) rotation and color flip operations per insert
• We will not discuss LLRB delete
  • Not too terrible really, but it's just not interesting enough to cover. See optional textbook if you're curious

LLRB Implementation

• Amazingly, turning BST into an LLRB requires only 3 clever lines of code
  • Does not include helper methods (which do not require cleverness)

Search Tree Summary

Search Tree

• In the last 3 lectures, we talked about using search trees to implement sets/maps
  • Binary search trees are simple, but they are subject to imbalance
  • 2-3 Trees (B Trees) are balanced, but painful to implement and relatively slow
  • LLRBs insertion is simple to implement (but delete is hard)
    • Works by maintaining mathematical bijection with a 2-3 trees
  • Java's TreeMap is a red-black tree (not left leaning)
    • Maintains correspondence with 2-3-4 tree (is not a 1-1 correspondence)
    • Allows glue links on either side
    • More complex implementation, but significantly faster
• There are many other types of search trees out there
  • Other self balancing trees: AVL trees, splay trees, treaps, etc.
• There are other efficient ways to implement sets and maps entirely
  • Other linked structures: Skip lists are linked lists with express lanes
  • Other ideas entirely: Hashing is the most common alternative. We'll discuss this idea in the next lecture

CSM Review

B-Trees

• B is for balanced
• Some definitions:
  • depth of a node is distance to the root (the root node has depth 0)
  • height of a tree is the depth of the lowest leaf
• Purpose of B-trees:
  • Avoids spindly trees
  • Keeps the tree with height log(n)

2-3 Trees

• Each non-leaf node can have 2 or 3 children
• Each node can be stuffed with at most 2 values
  • Once a node is overstuffed (aka 3 values), push middle value up

2-3-4 Trees

• Same idea as 2-3 trees, but now nodes can have 2, 3, or 4 children
• A node is overstuffed if it has 4 values
• Push up left-middle node

Traversals

• Level-Order Traversals: Nodes are visited top-to-bottom, left-to-right
• Depth-First Traversals: Visit deep nodes before shallow ones
• In-order Traversal: LFR - "Left, Functionality, Right"
  • In a BST, this produces a sorted list of nodes in the tree (an in-order traversal that is "depth-first search")

Rotating Nodes

• Imagine a circle around the node you rotate around and its child nodes
• "Pull" everything around in the direction you want to rotate
• Rotations do not change the in-order traversal

Left-Leaning Red Black Trees

• A binary search tree
• Has a 1-1 correlation with 2-3 trees
  • Values that are stuffed into one node are now connected with red links
• Invariant: all red edges lean to the left
  • Fix by rotation/color swap
• Insert nodes with a red link (in a 2-3 tree we stuff values in a leaf node)

Tree Traversals

• Depth First Search means we visit each subtree in some order recursively
  • Usually done with a stack
  • Pre Order
    • visit self, visit left, visit right
    • visit parent node before visiting child nodes
  • Post Order
    • visit left, visit right, visit self
    • visit left child, then parent, then right child
    • Can be done with a stack
  • In Order
    • visit left, visit self, visit right
    • visit child nodes before visiting parent nodes
• Level Order (Breadth First Search)
  • Visit in order of tree levels
  • Iterative search!
  • Usually done with a queue