Lecture 20: Hash Tables

10/12/2020

Data Indexed Arrays

Limits of Search Tree Based Sets

• Our search tree sets require items to be comparable
  • Need to be able to ask "is X < Y?" Not true of all types
  • Could we somehow avoid the need for objects to be comparable
• Search tree sets have excellent performance, but could maybe be better
  • Could we somehow do better than Theta(log N)?

Using Data as an Index

• One extreme approach: Create an array of booleans indexed by data!
  • Initially all values are false
  • When an item is added, set the appropriate index to true
    • i.e. 1F 2F 3T 4F 5F 6T 7F 8F ... is a set containing 3 and 6

public class DataIndexedIntegerSet {
    private boolean[] present;

    public DataIndexedIntegerSet() {
        present = new boolean[2000000000];
    }

    public add(int i) {
        present[i] = true;
    }

    public contains(int i) {
        return present[i];
    }
}

• Everything runs in constant time
• Downsides of this approach:
  • Extremely wasteful of memory. To support checking presence of all positive integers
  • Need some way to generalize beyond integers

DataIndexedEnglishWordSet

Generalizing the DataIndexedIntegerSet Idea

• Ideally, we want a data indexed set that can store arbitrary types
• The previous idea only supports integers!
  • Let's talk about storing Strings. We'll go into generics later
• Suppose we want to add ("cat")
• The key question:
  • What is the cat'th element of a list?
  • One idea: Use the first letter of the word as an index
• What's wrong with this approach?
  • Other words start with c
    • contains("chupacabra"): true ("chupacabra" collides with "cat")
  • Can't store "=98tu4it92"

Avoiding Collisions

• Use all digits by multiplying each by a a power of 27
  • Thus, the index of "cat" is (3 x 27^2) + (1 x 27^1) + (20 x 27^0) = 2234
• Why this specific pattern?
  • Let's review how numbers are represented in decimal

THe Decimal Number System vs. Our Own System for Strings

• In the decimal number system, we have 10 digits
• Want numbers larger than 9? Use a sequence of digits
• Our system for strings is almost the same, but with letters

Uniqueness

• As long as we pick a base >= 26, this algorithm is guaranteed to give each lowercase English word a unique number!
  • Using base 27, no words will get the number 1598
• In other words: Guaranteed that we will never have a collision

public class DataIndexedEnglishWordSet {
    private boolean[] present;

    public DataIndexedEnglishWordSet() {
        present = new boolean[2000000000];
    }

    public add(String s) {
        present[englishToInt(s)] = true;
    }

    public contains(String s) {
        return present[englishToInt(s)];
    }
}

DataIndexedStringSet

DataIndexedStringSet

• Using only lowercase English characters is too restrictive
  • To understand what value we need to use for our base, let's discuss briefly the ASCII standard
  • Maximum possible value for english-only text including punctuation is 126, so let's use 126 as our base in order to ensure unique values for possible strings

ASCII Characters

• THe most basic character set used by most computers is ASCII format
  • Each possible character is assigned a value between 0 and 127
  • Characters 33-126 are "printable", and are shown below
  • For example, char c = 'D' is equivalent to char c = 68

Implementing asciiToInt

• The corresponding integer conversion function is actually even simpler than englishToInt. Using the raw character value means we avoid the need for a helper method

Going Beyond ASCII

• chars in Java also support character sets for other languages like Chinese
  • This encoding is known as Unicode. Table is too big to list

Example: Computing Unique Representations of Chinese

• The largest possible value for chinese characters is 40959, so we'd need to use this as our base if we want to have a unique representation for all possible strings of Chinese characters

Integer Overflow and Hash Codes

Major Problem: Integer Overflow

• In Java, the largest possible integer is 2147483647
  • If you go over this limit, you overflow, starting back over at the smallest integer, which is -2147483647

Consequence of Overflow: Collisions

• Because Java has a maximum integer, we won't get the numbers we expect
  • With base 126, we will run into overflow even for short strings
    • Example: omens = 28196917171, which is much greater than the maximum integer
• Overflow can result in collisions, causing incorrect answers

Hash Codes and the Pigeonhole Principle

• The official term for the number we're computing is "hash code"
  • A has code "projects a value from a set with many (or even an infinite number of) members to a value from a set with a fixed number of (fewer) members"
  • Here, our target set is the set of Java integers, which is of size 4294967296
• Pigeonhole principle tells us that if there are more than 4294967296 possible items, multiple items will share the same hash code
• Hence, collisions are inevitable

Two Fundamental Challenges

• Two Fundamental Challenges
  • How do we resolve hashCode collisions
    • We'll call this collision handling
  • How do we compute a hash code for arbitrary objects?
    • We'll call this computing a hashCode

Hash Tables: Handling Collisions

Resolving Ambiguity

• Pigeonhole principle tells us that collisions are inevitable due to integer overflow
• Suppose N items have the same numerical representation h:
  • Instead of storing true in position h, store a "bucket" of these N items at position h
• How to implement a "bucket"?
  • Any type of list or set or data structure

The Separate Chaining Data Indexed Array

• Each bucket in our array is initially empty. When an item x gets added at index h:
  • If bucket h is empty, we create a new list containing x and store it at index h
  • If bucket h is already a list, we add x to this list if it is not already present
• We might call this a "separate chaining data indexed array"
  • Bucket #h is a "separate chain" of all items that have hash code h

Separate Chaining Performance

• Observation: Worst case runtime will be proportional to length of longest list
  • contains: Theta(Q)
  • insert: Theta(Q)
  • Q: Length of longest list

Saving Memory Using Separate Chaining

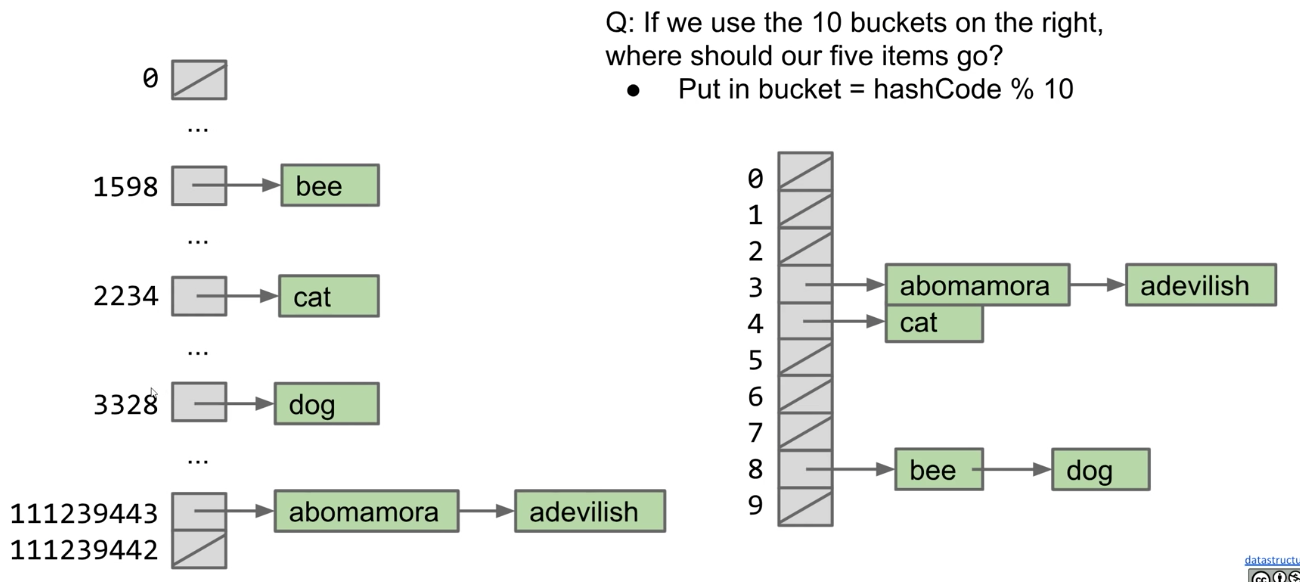
• Observation: We don't really need billions of buckets
  • If we use just 10 buckets, where should our items go?
• Observation: Can use modulus of hashcode to reduce bucket count
  • Put in bucket = hashCode % 10
  • Downside: Lists will be longer

The Hash Table

• What we've just created here is called a hash table
  • Data is converted by a hash function into an integer representation called a hash code
  • The hash code is then reduced to a valid index, usually using the modulus operator, e.g. 2348762878 % 10 = 8

Hash Table Performance

Hash Table Runtime

• The good news: We use way less memory and can now handle arbitrary data
• The bad news: Worst case runtime (for both contains and insert) is now Theta(Q), where Q is the length of the longest list
• For the has table with 5 buckets, the order of growth of Q with respect to N is Theta(N)
  • In the best case, the length of the longest list will be N/5. IN the worst case, it will be N. In both cases, Q(N) is Theta(N)

Improving the Hash Table

• Suppose we have:
  • A fixed number of buckets M
  • An increasing number of items N
• Major problem: Even if items are spread out evenly, lists are of length Q = N/M
  • How can we improve our design to guarantee that N/M is Theta(1)

Hash Table Runtime

• A solution:
  • An increasing number of buckets M
  • An increasing number of items N
• One example strategy: When N/M is >= 1.5, then double M
  • We often call this process of increasing M "resizing"
  • N/M is often called the "load factor". It represents how full the hash table is

Resizing Hash Table Runtime

• As long as M = Theta(N), then O(N/M) = O(1)
• Assuming items are evenly distributed, lists will be approximately N/M items long, resulting in Theta(N/M) runtimes
  • Our doubling strategy ensures that N/M = O(1)
  • Thus, worst case runtime for all operations if Theta(N/M) = Theta(1)
    • ... unless that operation causes a resize
• One important thing to consider is the cost of the resize operation
  • Resizing takes Theta(N) time. Have to redistribute all items
  • Most add operations will be Theta(1). SOme will be Theta(N) time (to resize)
    • Similar to our ALists, as long as we resize by a multiplicative factor, the average runtime will still be Theta(1)

Has Table Runtime

• Hash table operations are on average constant time if:
  • We double M to ensure constant average bucket length
  • Items are evenly distributed
  • contains: Theta(1) (Assuming all items are even spaced)
  • add: Theta(1) (On average)

Regarding Even Distribution

• Even distribution of items is critical for good hash table performance
• We will need to discuss how to ensure even distribution

Hash Tables in Java

The Ubiquity of Hash Tables

• Has tables are the most popular implementation for sets and maps
  • Great performance in practice
  • Don't require items to be comparable
  • Implementations often relatively simple
  • Python dictionaries are just hash tables in disguise
• In Java, implemented as java.util.HashMap and java.util.HashSet
  • How does a HashMap know how to compute each object's hash code?
    • Good news: It's not "implements Hashable"
    • Instead, all objects in Java must implement a .hashCode() method

Objects

• All classes are hyponyms of Object
  • int hashCode() (Default implementation simply returns the memory address of the object)

Examples of Real Java HashCodes

• We can see that Strings in Java override hasCode, doing something vaguely like what we did earlier
  • Will see the actual hashCode() function later

"a".hashCode()  // 97
"bee".hashCode()  // 97410

Using Negative hash codes

• Suppose that we have a hash code as -1
  • Given a hash table of length 4, we should put this object in bucket 3
  • Unfortunately, -1 % 4 = -1. Will result in index errors!
  • Use Math.floorMod instead

-1 % 4  // -1
Math.floorMod(-1, 4)  // 3

Hash Tables in Java

• Java hash tables:
  • Data is converted by the hashCode method an integer representation called a hash code
  • The hash code is then reduced to a valid index, using something like the floorMod function

Two Important Warnings When Using HashMaps/HashSets

• Warning #1: Never store objects that can change in a HashSet or HashMap!
  • If an object's variables changes, then its hasCode changes. May result in items getting lost.
• Warning #2: Never override equals without also overriding hashCode
  • Can also lead to items getting lost and generally weird behavior
  • HasMaps and HashSets use equals to determine if an item exists in a particular bucket

Good HashCodes

What Makes a good hashCode()?

• Goal: We want has tables that are evenly distributed
  • Want a hasCode that spreads things out nicely on real data
    • Returning string treated as a base B number can be good
  • Writing a good hashCode() method can be tricky

Hashbrowns and Hash Codes

• How do you make hashbrowns?
  • Chopping a potato into nice predictable segments? No way!
  • Similarly, adding up the characters is not nearly "random" enough
• Can think of multiplying data by powers of some base as ensuring that all the data gets scrambled together into a seemingly random integer

Example hasCode Function

• The Java 8 hash code for strings. Two major differences from our hash codes:
  • Represents strings as a base 31 number
    • Why such a small base? Real hash codes don't care about uniqueness
  • Stores (caches) calculated has code so future hashCode calls are faster

@Override
public int hasCode() {
    int h = cachedHashValue;
    if (h == 0 && this.length() > 0) {
        for (int i = 0; i < this.length; i++) {
            h = 31 * h + this.charAt(i);
        }
        cachedHasValue = h;
    }
    return h;
}

Example: Choosing a Base

• Which is better? ASCII's base 126 or Java's base 31
  • Might seem like 126 is better. Ignoring overflow, this ensures a unique numerical representation for all ASCII strings
  • ... but overflow is a particularly bad problem for base 126!
    • Any string that ends in the same last 32 characters has the same has code
      • Why? Because of overflow
      • Basic issue is that 126^32 = 126^33 = 126^34 = ... = 0
        • Thus upper characters are all multiplied by zero
        • See CS61C for more

Typical Base

• A typical hash code base is a small prime
  • Why prime?
    • Never even: Avoids the overflow issue on previous slide
    • Lower chance of resulting hasCode having a bad relationship with the number of buckets
  • Why small?
    • Lower cost to compute

Hashbrowns and Hash Codes

• Using a prime base yields better "randomness" than using something like base 126

Example: Hashing a Collection

• Lists are a lot like strings: Collection of items each with its own hashCode:

@Override
public int hashCode() {
    int hashCode = 1;
    for (Object o : this) {
        hashCode = hashCode * 31;  // elevate/smear the current hash code
        hashCode = hashCode + o.hashCode();  // add new item's hash code
    }
    return hashCode
}

• To save time hashing: Look at only first few items
  • Higher chance of collisions but things will still work

Example: Hashing a Recursive Data Structure

• Computation of the hashCode of a recursive data structure involves recursive computation
  • For example, binary tree hashCode (assuming sentinel leaves):

@Override
public int hashCode() {
    if (this.value == null) {
        return 0;
    }
    return this.value.hashCode() + 
    31 * this.left.hashCode() + 
    31 * 31 * this.right.hashCode();
}

Summary

Hash Tables in Java

• Hash tables:
  • Data is converted into a hash code
  • The hash code is then reduced to a valid index
  • Data is then stored in a bucket corresponding to that index
  • Resize when load factor N/M exceeds some constant
  • If items are spread out nicely, you get Theta(1) average runtime