Lecture 21: Heaps and PQs

10/14/2020

The Priority Queue Interface

The Priority Queue Interface

/** (Min) Priority Queue: Allowing tracking and removal of the
  * smallest item in a priority queue */
public interface MinQP<Item> {
    // Adds the item to the priority queue
    public void add(Item x);

    // Returns the smallest item in the priority queue
    public Item getSmallest();

    // Removes the smallest item from the priority queue
    public Item removeSmallest();

    // Returns the size of the priority queue
    public int size();
}

• Useful if you want to keep track of the "smallest", "largest", "best" etc. seen so far

Usage example: Unharmonious Text

• Imagine that you're part of the US Happiness Enhancement team
  • Your job: Monitor text messages of the citizens to make sure they are not having any unharmonious conversations
  • Prepare a report of M messages that seem most unharmonious
• Naive approach: Create a list of all messages sent for the entire day. Sort it using your comparator. Return the M messages that are largest

Naive Implementation: Store and Sort

• Potentially uses a huge amount of memory Theta(N), where N is number of texts
  • Goal: Do this in Theta(M) memory using a MinPQ
  • MinPQ<String> unharmoniousTexts = new HeapMinPQ<Transaction>(cmptr);

Better Implementation: Track the M Best

• Can track top M transactions using only M memory. API for MinPQ also makes code very simple (don't need to do explicit comparisons)

How Would we Implement a MinPQ?

• Some possibilities:
  • Ordered Array
    • add: Theta(N)
    • getSmallest: Theta(1)
    • removeSmallest: Theta(N)
  • Bushy BST: Maintaining bushiness is annoying. Handling duplicate priorities is awkward
    • add: Theta(log N)
    • getSmallest: Theta(log N)
    • removeSmallest: Theta(log N)
  • HashTable: No good! Items go into random places

Heaps

Introducing the Heap

• BSTs would work, but need to be kept bushy and duplicates are awkward
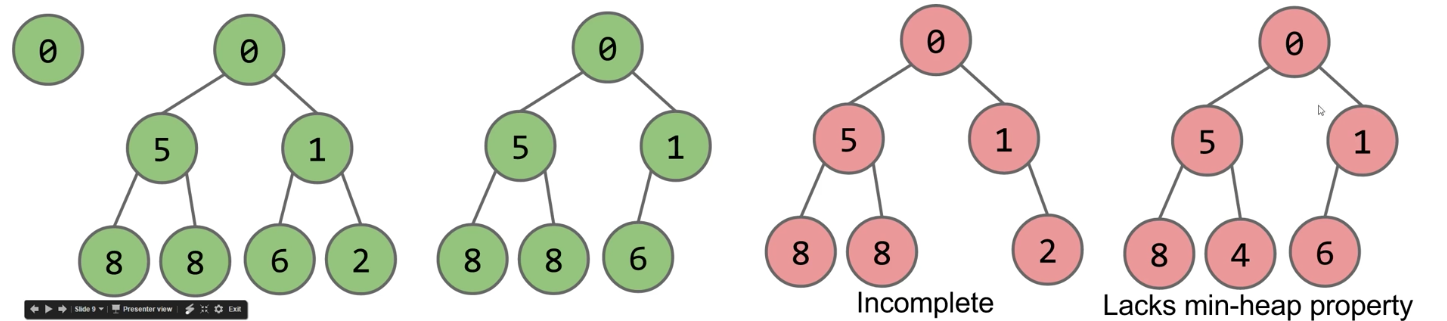
• Binary min-heap: Binary tree that is complete and obeys min-heap property
  • Min-heap: Every node is less than or equal to both of its children
  • Complete: Missing items only at the bottom level (if any), all nodes are as far left as possible

What Good are Heaps?

• Heaps lend themselves very naturally to implementation of a priority queue
• Questions:
  • How would you support getSmallest()
    • Return the root

How Do We Add to a Heap?

• Challenge: Come up with an algorithm for add(x)
  • How would we insert 3?
  
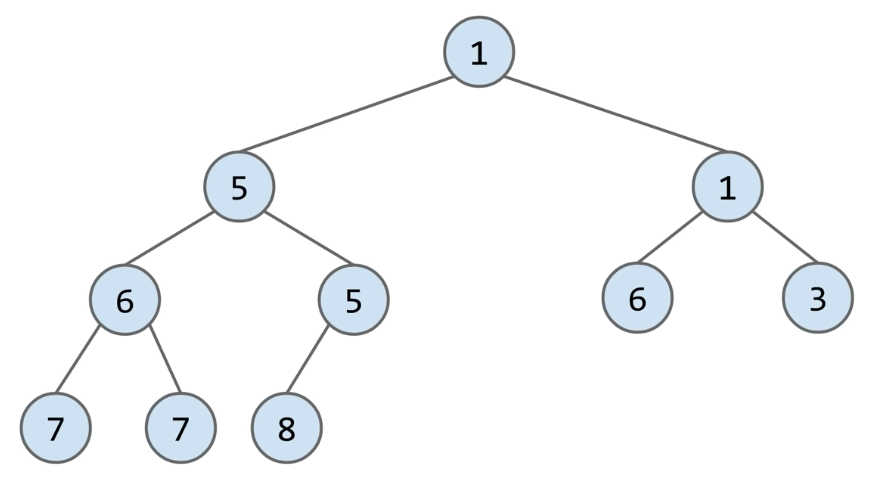
  • Add to end of heap temporarily
  • Swim up to the hierarchy to rightful place
  
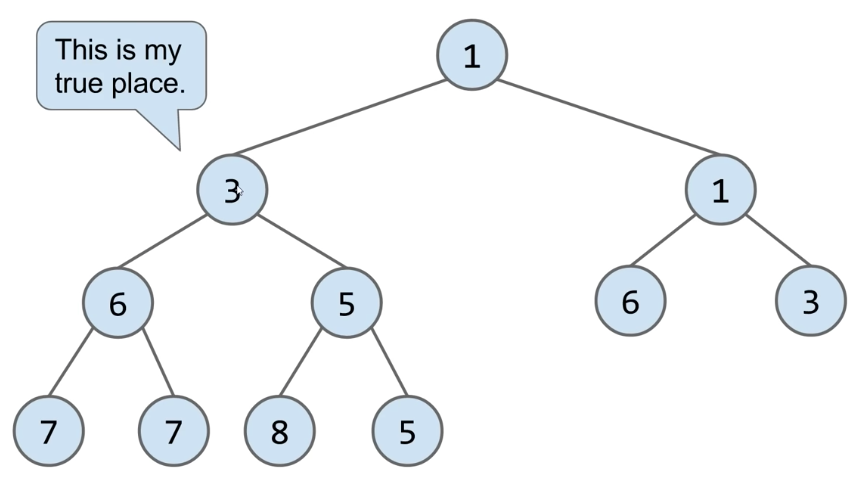
  • Delete min
    • Swap the last item in the heap into the root
    • Then sink your way down the hierarchy, yielding to the most "qualified" items

Heap Operations Summary

• Given a heap, how do we implement PQ operations?
  • getSmallest() - return the item in the root node
  • add(x) - place the new employee in the last position, and promote as high as possible
  • removeSmallest() - assassinate the president (of the company), promote the rightmost person in the company to president. Then demote repeatedly, always taking the "better"successor

Tree Representations

How do we represent a tree in Java?

• Approach 1a, 1b, and 1c: Create mapping from node to children

public class Tree1A<Key> {
    Key k;
    Tree1A left;
    Tree1A middle;
    Tree1A right;
}

public class Tree1B<Key> {
    Key k;
    Tree1B[] children;
    ...
}

// Sibling tree
public class Tree1C<Key> {
    // Nodes at the same level point to each other's siblings
    Key k;
    Tree1C favoredChild;
    Tree1C sibling;
}

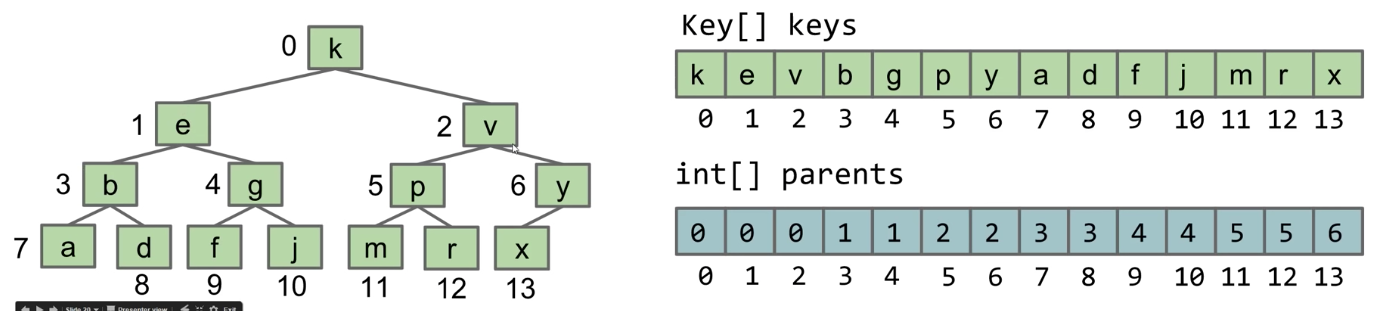
• Approach 2: Store keys in an array. Store parentIDs in an array
  • Similar to what we did with disjointSets

public class Tree2<Key> {
    Key[] keys;
    int[] parents;
    ...
}

• Approach 3: Store keys in an array. Don't store structure anywhere
  • To interpret array: Simply assume tree is complete
  • Obviously only works for "complete" trees

public class Tree3<Key> {
    Key[] keys;
}

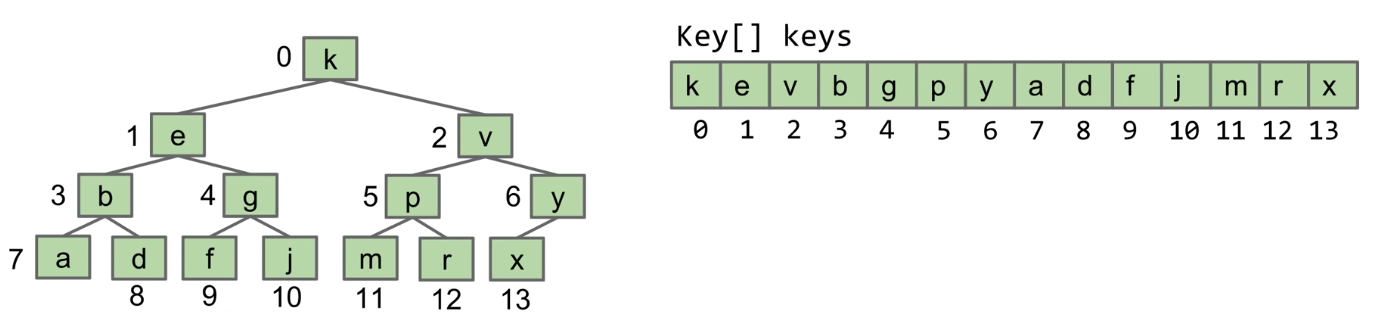
A Deep Look at Approach 3

• Write the parent(k) method for approach 3

public void swim(int k) {
    if (keys[parent(k)] > keys[k]) {
        swap(k, parent(k));
        swim(parent(k));
    }
}

public int parent(int k) {
    if (k == 0) {
        return 0;
    }
    return (k - 1) / 2;
}

Approach 3B (book implementation): Leaving One Empty Spot in the Front

• Approach 3b: Store keys in an array. Offset everything by 1 spot
  • Same as 3, but leave spot 0 empty
  • Makes computation of children/parents "nicer"
    • leftChild(k) = k * 2
    • rightChild(k) = k * 2 + 1
    • parent(k) = k / 2

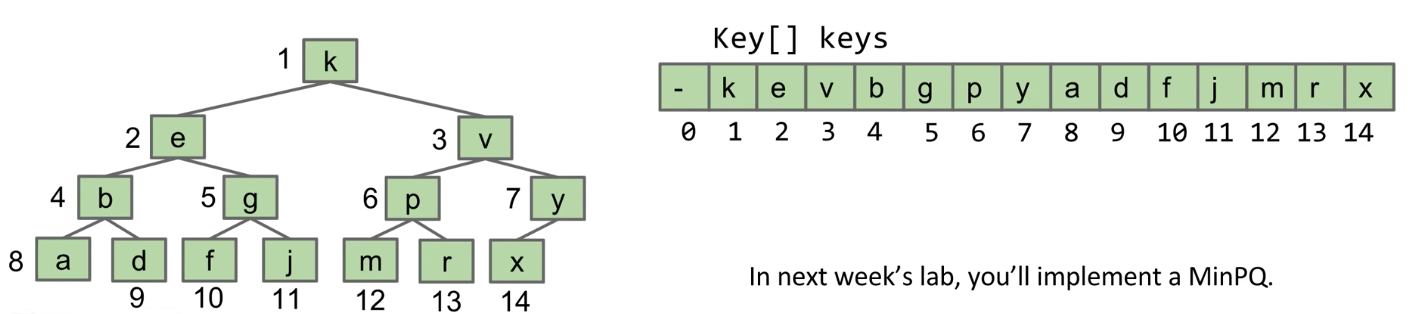
Heap Implementation of a Priority Queue

• Heap
  • add: Theta(log N)
  • getSmallest: Theta(1)
  • removeSmallest: Theta(log N)
• Notes:
  • Why "priority queue"? Can think of position in tree as its "priority"
  • Heap is log N time AMORTIZED (some resizes, but no big deal)
  • BST can have constant getSmallest if you keep a pointer to smallest
  • Heaps handle duplicate priorities much more naturally than BSTs
  • Array based heaps take less memory (very roughly about 1/3) the memory of representing a tree with approach 1a)

Some Implementation Questions

• How does a PQ know how to determine which item in a PQ is larger?
  • What could we change so that there is a default comparison?
• What constructors are needed to allow for different orderings?

Data Structures Summary

The Search Problem

• Given a stream of data, retrieve information of interest
  • Examples:
    • Website users post to personal page. Serve content only to friends
    • Given logs for thousands of weather stations, display weather map for specified date and time

Search Data Structures (The particularly abstract ones)

• Abstraction often happens in layers!
  • PQ -> Heap Ordered Tree -> Tree -> {Approach 1A, 1B, 1C, 2, 3, 3B}
  • External Chaining HT -> Array of Buckets -> Bucket -> {ArrayList, Resizing Array, LinkedList, BST (requires comparable items)}
• Specialized searching data structures:

Data Structures

• Data Structure: A particular way of organizing data
  • We've covered many of the most fundamental abstract data types, their common implementations, and the tradeoffs thereof

Summary

Discussion Summary: Heaps

• Heaps are special trees that follow a few basic rules:
  • Heaps are complete - the only empty parts of a heap are in the bottom row, to the right
  • In a min-heap, each node must be smaller than all of its child nodes. The opposite is true for max-heaps