Prefix Operations and Tries

10/16/2020

Tries

Abstract Data Types vs. Specific Implementations

• There are many ways to implement an abstract data type
  • Today we'll talk about a new way to build a set/map

BST and Hash Table Set Runtimes

• Runtimes for our balanced search tree and has table implementations were very fast
• If we know that our keys all have some common special property, we can sometimes get even better implementations
• Suppose we know that our keys are always single ASCII characters

Special Case 1: Character Keyed Map

• Suppose we know that our keys are always ASCII characters
  • Can just use an array!
  • Simple and fast

public class DataIndexedCharMap<V> {
    private V[] items;
    public DataIndexedCharMap(int R) {
        items = (V[]) new Object[R];
    }
    public void put(char c, V val) {
        items[c] = val;
    }
    public V get(char c) {
        return items[c];
    }
}

• Constant time for both get and add

Special Case 2: String Keyed Map

• Suppose we know that our keys are always strings
  • Can use a special data structure known as a Trie
  • Basic idea: Store each letter of the string as a node in a tree
• Tries will have great performance on:
  • get
  • add
  • special string operations

Sets of Strings

• For String keys, we can use a "Trie". Key ideas:
  • Every node stores only one letter
  • Nodes can be shared by multiple keys
  

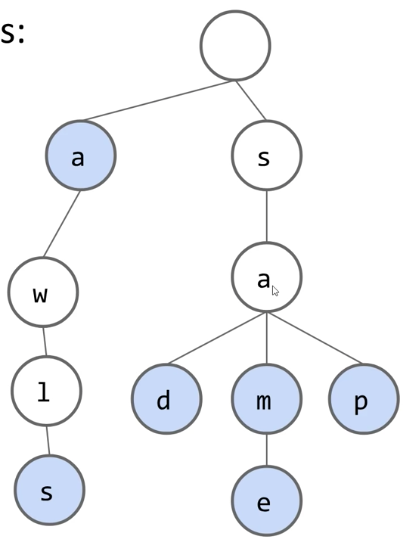
Tries: Search Hits and Misses

• How does contains work?
  • contains("sam"): true, blue node (hit)
  • contains("sa"): false, white node (miss)
  • contains("a"): true, blue node (hit)
  • contains("saq"): false, fell off tree (miss)
• Two ways to have a search "miss":
  • If the final node is white
  • If we fall off the tree, e.g. contains("sax")

Trie Maps

• Tries can also be maps, of course

Tries

• Trie:
  • Short for Retrieval Tree
  • Inventor Edward Fredkin suggested it should be pronounced "tree", but almost everyone pronounces it like "try"

Trie Implementation and Performance

Very Basic Trie Implementation

• The first approach might look something like the code below
  • Each node stores a letter, a map from c to all child nodes, and a color

public class TrieSet {
    private static final int R = 128;  // ASCII
    private Node root;  // root of trie

    private static class Node {
        private char ch;  // Actually don't need this variable
        private boolean isKey;
        private DataIndexedCharMap next;
        private Node(char c, boolean b, int R) {
            ch = c; isKey = b;
            next = new DataIndexedCharMap<Node>(R);
        }
    }
}

• For each node in DataIndexedCharMap, there are 128 links

Trie Performance in Terms of N

• Given a Trie with N keys. What is the:
  • Add runtime?
    • Theta(1)
  • Contains runtime?
    • Theta(1)
• Runtimes independent of number of keys!
• Or in terms of L, the length of the key:
  • Add: Theta(L)
  • Contains: O(L)
    • May fall off the tree
• When our keys are strings, Tries give us slightly better performance on contains and add
• One downside of the DictCharKey based Trie is the huge memory cost of storing R links per node (most of which are null)
  • Wasteful because most links are not used in real world usage

Alternate Child Tracking Strategies

DataIndexedCharMap Trie

• Can use ANY kind of map from character to node, e.g.
  • BST
  • Hash Table
• Fundamental problem, our arrays are "sparse", wasted memory boxes

Alternate Idea #1: The Hash-Table Based Trie

Alternate Idea #2: The BST-Based Trie

The Three Trie Implementations

• When we implement a Trie, we have to pick a map to our children
  • DataIndexedCharMap: Very fast, but memory hungry
  • Hash Table: Almost as fast, uses less memory
  • Balanced BST: A little slower than Hash Table, uses similar amount of memory

Performance of the DataIndexedCharMap, BST, and Hash Table

• Using a BST or a Hash Map to store links to children will usually use less memory
  • DataIndexedCharMap: 128 links per node
  • BST: C links per node, where C is the number of children
  • Hash Table: C links per node
  • Note: Cost per link is higher in BST and Hash Table
• Using a BST or a Hash Table will take slightly more time
  • DataIndexedCharMap is Theta(1)
  • BST is O(log R), where R is size of alphabet
  • Hash Table is O(R), where R is size of alphabet
• Since R is fixed (e.g. 128), can think of all 3 as Theta(1)

Trie Performance in Terms of N

• When our keys are strings, Tries give us slightly better performance on contains and add
  • Using BST or Hash Table will be slightly slower, but more memory efficient
  • Would have to do computational experiments to see which is best for your application
• ...but where Tries really shine is their efficiency with special string operations!

Trie String Operations

String Specific Operations

• Theoretical asymptotic speed improvement is nice. But the main appeal of tries is their ability to efficiently support string specific operations like prefix matching
  • Finding all keys that match a given prefix: keysWithPrefix("sa")
  • Finding the longest prefix of a string: longestPrefixOf("sample")

Collecting Trie Keys

• Give an algorithm for collecting all the keys in a Trie
• collect():
  • Create an empty list of results x
  • For character c in root.next.keys():
    • Call colHelp("c", x, root.next.get(c))
  • Return x
• Create colHelp
  • colHelp(String s, List x, Node n)
  • If n.isKey, then x.add(s)
  • For character c in n.next.keys():
    • Call colHelp(s + c, x, n.next.get(c))

Usages of Tries

• Give an algorithm for keysWithPrefix
• keysWithPrefix(prefix):
  • Find the node A corresponding to the string
  • Create an empty list x
  • For character c in A.next.keys():
    • Call colHelp(prefix + c, x, A.next.get(c))
• Another common operation: LongestPrefixOf

Autocomplete

The Autocomplete Problem

• One way to do this is to create a Trie based map from strings to values
  • Value represents how important Google thinks that string is
  • Can store billions of strings efficiently since they share nodes
  • When a user types in a string "hello", we:
    • Call keysWithPrefix("hello")
    • Return the 10 strings with the highest value
• The approach has one major flaw. If we enter a short string, the number of keys with the appropriate prefix will be too big

A More Efficient Autocomplete

• One way to address this issue:
  • Each node stores its own value, as well as the value of its best substring
• Search will consider nodes in the order of "best"
  • Can stop when top 3 matches are all better than best remaining
• Details left as an exercise. Hint: Use a PQ! See Bear Maps gold points for more

Even More Efficient Autocomplete

• Can also merge nodes that are redundant where there's no branching!
  • This version of trie is known as a "radix tree" or "radix trie"
  • Won't discuss

Trie Summary

Tries

• When your key is a string, you can use a Trie:
  • Theoretically better performance than hash table or search tree
  • Have to decide on a mapping from letter to node. Three natural choices:
    • DataIndexedCharMap, i.e. an array of all possible child links
    • Bushy BST
    • Hash Table
  • All three choices are fine, though hash table is probably the most natural
  • Supports special string operations like longestPrefixOf and keysWithPRefix
    • keysWithPrefix is the heart of important technology like autocomplete
    • Optimal implementation of Autocomplete involves use of a priority queue!

Domain Specific Sets and Maps

• More generally, we can sometimes take special advantage of our key type to improve our sets and maps
  • Example: Tries handle String keys. Allow for fast string specific operations
  • Note: There are many other types of string sets/maps out there

Discussion Summary: Tries

• Tries are special trees mostly used for language tasks
• Each node in a trie is marked as being a word-end or not, so you can quickly check whether a word exists within your structure