Lecture 25: Shortest Paths
10/23/2020
Graph Problems
BFS vs. DFS for Path Finding
- Possible considerations:
- Correctness. Do both work for all graphs?
- Output Quality. Does one give better results?
- BFS is a 2-for-1 deal, not only do you get paths, but your paths are also guaranteed to be shortest
- Time Efficiency. Is one more efficient than the other?
- Should be very similar. Both consider all edges twice
- Space Efficiency. Is one more efficient than the other?
- DFS is worse for spindly graphs
- Call stack gets very deep
- Computer needs Theta(V) memory to remember recursive calls
- BFS is worse for absurdly "bushy" graphs
- Queue gets very large. In worst case, queue will require Theta(V) memory
- Note: In our implementations, we have to spend Theta(V) memory anyway to track distTo and edgeTo arrays
Breadth FirstSearch for Google Maps
- BFS would not be a good choice for a google maps style navigation application
- We need an algorithm that takes into account edge distances, also known as "edge weights"
Dijkstra's Algorithm
Single Source Single Target Shortest Paths
- Observation: Solution will always be a path with no cycles (assuming non-negative weights)
Problem: Single Source Shortest Paths
- Goal: Find the shortest paths from source vertex s to every other vertex
- Observation: Solution will always be a tree
- Can think of as the union of the shortest paths to all vertices
Edge Count
- If G is a connected edge-weighted graph with V vertices and E edges, how many edges are in the Shortest Paths Tree (SPT) of G? [assume every vertex is reachable]
- Since the solution is a tree, there are V-1 edges
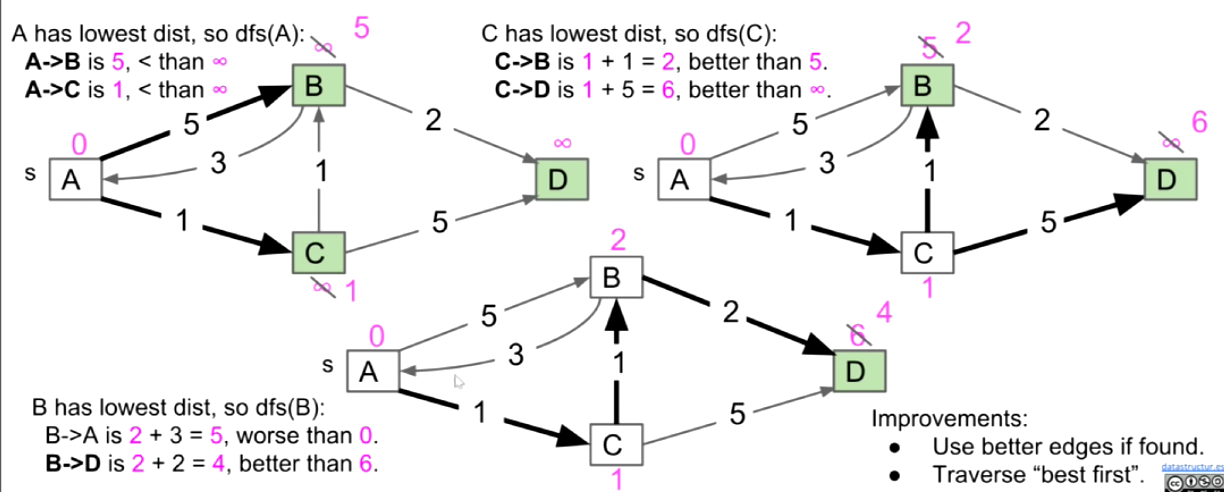
Creating an Algorithm
- Start with a bad algorithm
- Algorithm begins with all vertices unmarked and all distance infinite. No edges in the shortest paths tree (SPT)
- Bad algorithm #1: Perform a depth first search. When you visit v:
- For each edge from v to w, if w is not already part of SPT, add the edge
- Bad algorithm #2: Perform a depth first search. When you visit v:
- For each edge from v to w, add edge to the SPT only if that edge yields better distance (we'll call this process "edge relaxation")
- Improvements:
- Use better edges if found
Dijkstra's Algorithm
- Perform a best first search (closest first). When you visit v:
- For each v to w, relax that edge
- Improvements:
- Use better edges if found
- Traverse "best first"
- Insert all vertices into fringe PQ (e.g. use a heap), storing vertices in order of distance from source
- Repeat: Remove (closest) vertex v from PQ, and relax all edges pointing from v
- Note: If non-negative weights, impossible for any inactive vertex (i.e. already visited and not on the fringe) to be improved
- Would result in a cycle if it does

Dijkstra's Correctness and Runtime
Dijkstra's Algorithm Pseudocode
- Dijkstra's:
- PQ.add(source, 0)
- For other vertices v, PQ.add(v, infinity)
- While PQ is not empty:
- p = PQ.removeSmallest()
- Relax all edges from p
- Relaxing and edge p -> q with weight w:
- If distTo[p] + w < distTo[q]:
- distTo[q] = distTo[p] + w
- edgeTo[q] = p
- PQ.changePriority(q, distTo[q])
- Key invariants:
- edgeTo[v] is the best known predecessor of v
- distTo[v] is the best known total distance from source to v
- PQ contains all unvisited vertices in order of distTo
- Important properties:
- Always visits vertices in order of total distance from source
- Relaxation always fails on edges to visited (white) vertices
Guaranteed Optimality
- Dijkstra's Algorithm
- Visit vertices in order of best-known distance from source. On visit, relax every edge from the visited source
- Guaranteed to return a correct result if all edges are non-negative
- Proof relies on the property that relaxation always fails on edges to visited vertices
- Proof sketch: Assume all edges have non-negative weights
- At start, distTo[source] = 0, which is optimal
- After relaxing all edges from source, let vertex v1 be the vertex with minimum weight, i.e. that is closest to the source. Claim: distTo[v1] is optimal, and thus future relaxations will fail. Why?
- distTo[p] >= distTo[v1] for all p, therefore
- distTo[p] + w >= distTo[v1]
- Can use induction to prove that this holds for all vertices after dequeuing
Negative Edges
- Dijkstra's Algorithm
- Visit vertices in order of best-known distance from source. On visit, relax every edge from the visited vertex
- Dijkstra's can fail if graph has negative weight edges
- Relaxation of already visited edges can succeed
Dijkstra's Algorithm Runtime
- Priority Queue operation count, assuming binary heap based PQ:
- add: V, each costing O(log V) time
- removeSmallest: V, each costing O(log V) time
- changePriority: E, each costing O(log V) time
- Overall runtime: O(V*log(V) + V*log(V) + E*log(V))
- Assuming E > V, this is just O(E log V) for a connected graph
A*
Single Target Dijkstra's
- Is this a good algorithm for a navigation application
- Will it find the shortest path?
- Will it be efficient
- No. It will look for shortest path to other places
The Problem with Dijkstra's
- We have only a single target in mind, so we need a different algorithm. How can we do better?
How can we do better?
- Explore one direction first?
Introducing A*
- Simple idea:
- Visit vertices in order of d(Denver, v) + h(v, goal), where h(v, goal) is an estimate of the distance from v to our goal NYC
- In other words, look at some location if:
- We already know the fastest way to reach v
- AND we suspect that v is also the fastest way to NYC taking into account the time to get to v
- Observations:
- Not every vertex gets visited
- Result is not a shortest paths tree for a vertex, but that's OK since we only care about a path to a single vertex
A* Heuristic Example
- How do we get our estimate?
- Estimate is an arbitrary heuristic h(v, goal)
- heuristic: "using experience to learn and improve"
- Doesn't have to be perfect
A* Heuristics (Not covered in this class)
Heuristics and Correctness
- Four our version of A* to give the correct answer, out A heuristic must be:
- Admissible: h(v, NYV) <= true distance from v to NYC
- Consistent: For each neighbor of w:
- h(v, NYV) <= dist(v, w) + h(w, NYC)
- Where dist(v, w) is the weight of the edge from v to w
Consistency and Admissibility (Beyond scope)
- All consistent heuristics are admissible
- "Admissible" means that the heuristic never overestimates
Summary
Summary: Shortest Paths Problems
- Single source, multiple targets:
- Can represent shortest path from start to every vertex as a shortest paths tree with V-1 edges
- Can find the SPT using Dijkstra's algorithm
- Single source, single target:
- Dijkstra's is inefficient (searches useless parts of the graph)
- Can represent shortest path as path (with up to V-1 vertices, but probably far fewer)
- A* is potentially much faster than Dijkstra's
- Consistent heuristic guarantees correct solution



