Lecture 34: Sorting and Algorithmic Bounds

11/16/2020

Sorting

• Sorting is a foundational problem
  • Useful for putting things in order
  • But can be used to solve other tasks, sometimes in non-trivial ways
    • Sorting improves duplicate finding from a naive N^2 to N log N
    • Sorting improves 3SUM from a naive N^3 to N^2
  • There are many ways to sort an array, each with its own interesting tradeoffs and algorithmic features
• Today we'll discuss the fundamental nature of the sorting problem itself: How hard is it to sort?

Sorts Summary

Math Problems out of Nowhere

A Math Problem out of Nowhere

• Consider the functions N! and (N/2)^(N/2)
• Is N! \in Omega((N/2)^(N/2))?
  • Can experiment and find that the above statement is true

Another Math Problem

• Given that N! > (N/2)^(N/2), show that log(N!) \in Omega(N log N)
  • We have that N! > (N/2)^(N/2)
  • Taking the log of both sides, we can show the above statement
• In other words, log(N!) grows at least as quickly as N log N

Last Math Problem

• Show that N log N \in Omega(log(N!))
  • log(N!) = log(N) + log(N-1) + log(N-2) + ... + log(1)
  • N log N = log(N) + log(N) + log(N) + ... + log(N)
  • Hence, N log N \in Omega(log(N!))

Omega and Theta

• Given:
  • log(N!) \in Omega(N log N)
  • N log N \in Omega(log(N!))
• We can conclude that:
  • log(N!) \in Theta(N log N) AND
  • N log N \in Theta(log(N!))

Theoretical Bounds on Sorting

Sorting

• We have shown several sorts to require Theta(N log N) worst case time
  • Can we build a better sorting algorithm?
• Let the ultimate comparison sort (TUCS) be the asymptotically fastest possible comparison sorting algorithm, possibly yet to be discovered, and let R(N) be its worst case runtime in Theta notation
  • Comparison sort means that it uses the compareTo method in Java to make decisions
  • Worst case rn-time of TUCS, R(N), is O(N log N)
    • We already have algorithms that take Theta(N log N) worst case
  • Worst case run-time of TUCS, R(N) is Omega(1)
    • Obvious: Problem doesn't get easier than N
    • Can we make a stronger statement than Omega(1)?
  • Worst case run-time of TUCS, R(N), is also Omega(N)
    • Have to at least look at every item
  • But, with a clever argument, we can see that the lower bound will turn out to be Omega(N log N)
    • This lower bound means that across the infinite space of all possible ideas that any human might ever have for sorting using sequential comparisons, NONE has a worst case runtime that is better than N log N

The Game of Puppy, Cat, Dog

• Suppose we have a puppy, a cat, and a dog, each in an opaque soundproof box labeled A, B, and C. We want to figure out which is which using a scale

• We have to weigh a and c to resolve the final ambiguity

Puppy, Cat, Dog - A Graphical Picture of N = 3

• The full decision tree for puppy, cat, dog:

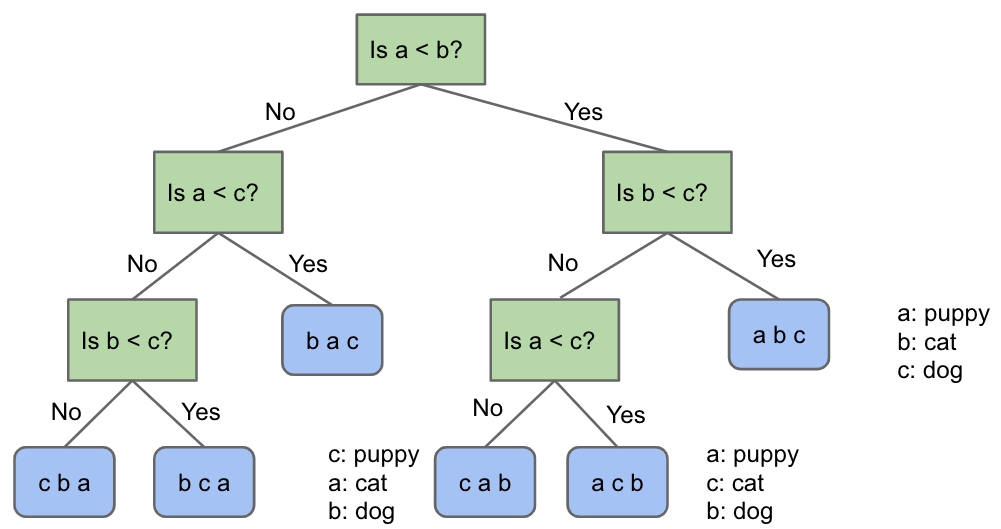
The Game of Puppy, Cat, Dog

• How many questions would you need to ask to definitely solve the "puppy, cat, dog, walrus" question?
  • If N = 4, we have 4! = 24 permutations of puppy, cat, dog, walrus
  • So we need a binary tree with 24 leaves
    • How many levels minimum? log_2(24) = 4.5, so 5 is the minimum
  • So at least 5 questions

Generalized Puppy, Cat, Dog

• How many questions would you need to ask to definitely solve the generalized "puppy, cat, dog" problem for N items?
  • Give your answer in big Omega notation
• Answer: Omega(log(N!))
  • For N, we have the following argument:
    • Decision tree needs N! leaves
    • So we need log_2(N!) rounded up levels, which is Omega(log(N!))

Generalizing Puppy, Cat, Dog

• Finding an optimal decision tree for the generalized version of puppy, cat, dog is an open problem in mathematics
• Deriving a sequence of yes/no questions to identify puppy, cat, dog is hard. An alternate approach to solving the puppy, cat, dog algorithm
  • Sort the boxes using any generic sorting algorithm
    • Leftmost box is puppy
    • Middle box is cat
    • Right box is dog

Sorting, Puppies, Cats, and Dogs

• A solution to the sorting problem also provides a solution to puppy, cat, dog
  • In other words, puppy, cat, dog reduces to sorting
  • Thus, any lower bound on difficulty of puppy, cat, dog must ALSO apply to sorting

Sorting Lower Bound

• We have a lower bound on puppy, cat, dog, namely it takes Omega(log(N!)) comparisons to solve such a puzzle
• Since sorting with comparisons can be used to solve puppy, cat, dog, then sorting also takes Omega(log(N!)) comparisons
• Or in other words:
  • Any sorting algorithm using comparisons, no matter how clever, must use at least k = log_2(N!) compares to find the correct permutation. So even TUCS takes at least log_2(N!) comparisons
  • log_2(N!) is trivially Omega(log(N!)), so TUCS must take Omega(log(N!)) time
• Earlier, we showed the log(N!) \in Theta(N log N), so we have that TUCS is Omega(N log N)
  • Any comparison based sort requires at least order N log N comparisons
• Proof summary:
  • Puppy, cat, dog is Omega(log_2(N!)), i.e. requires log_2(N!) comparisons
  • TUCS can solve puppy, cat, dog, and thus takes Omega(log_2(N!)) compares
  • log_2(N!) is Omega(N log N)
    • This was because N! is Omega((N/2)^(N/2))

Optimality

• The punchline:
  • Our best sorts have achieved absolute asymptotic optimality
    • Mathematically impossible to sort using fewer comparisons
    • Note: Randomized quicksort is only probabilistically optimal, but the probability is extremely high for even modest N. So don't worry about quicksort